Is Zero A Number? Was It Always A Number?

Is zero a number? Was it always a number?
Today, zero has two roles: First, as a placeholder within our number system, representing an absence of a value. It allows us to create huge numbers without extra digits. Its second role is as a number in its own right, in between -1 and 1. We can subtract, add, multiply by 0… but dividing gets tricky. I mean, you can’t divide 1 chicken by 0 chickens:

(You might think the answer would be infinity chickens, but it’s not, as infinity is a concept, not a number)

Most ancient civilisations developed some sort of number system to keep track of things, and they are all thought to have had a general concept of zero.

And when the Indians began developing a number system (the one that evolved into what we use today), zero was first explicitly born, with 9 number symbols and a dot to represent the absence of a number.

In the 7th Century, Brahmagupta developed terms for zero in addition, subtraction and division… though he struggled a bit with that last one.

Over time, the mathematics of India matured and spread outwards. But it found resistance in Europe, in particular against the established Roman numeral system.

But by the 13th century academics like Fibonacci were championing zero, helping it gain a solid foothold across Europe:
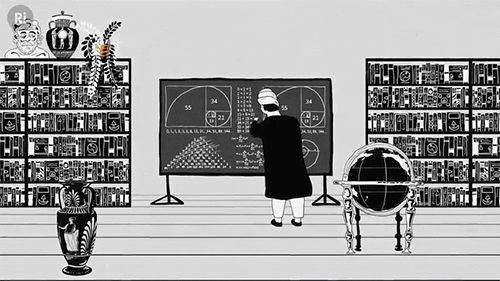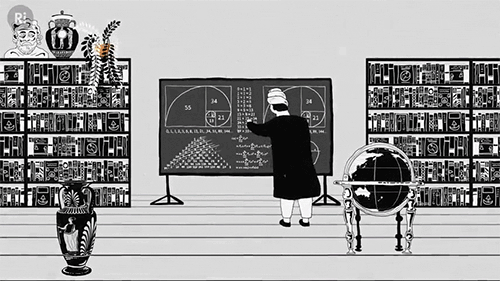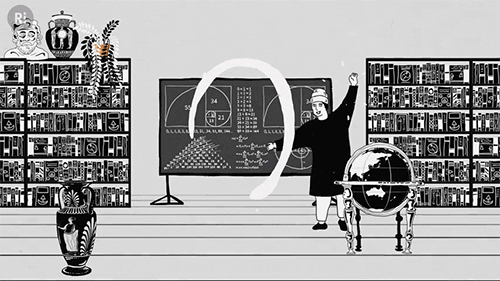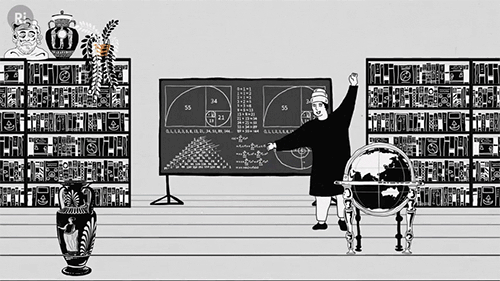
Zero went on to form the cornerstone of calculus, which allowed anyone to break down dynamic systems into smaller and smaller units approaching zero, but never quite getting there, avoiding the tricky problem of dividing by zero.

More recently, the binary numerical system formed the basis of the computer system and zero’s importance shone once more.

So maybe it really is possible to get something from nothing. Watch the full animation on our YouTube channel here.
More Posts from Mexmath and Others
![Graph Of Sine/cosine From Unit Circle. [via]](https://64.media.tumblr.com/bfa96325f13d0ba29cdb120618a81b95/tumblr_o3rv3pu4Tu1qcbrp0o1_500.gif)
Graph of sine/cosine from unit circle. [via]
What do you call a snake that’s exactly 3.14 feet long?

Question and solution from Lecture Notes on Mathematical Olympiad Courses For Junior Section by Xu Jiagu
EDIT FOR BS: Looks like a hazy memory and some dubious source) make for an ridiculously overexaggerated story. Ars Magna (published beforehand) seems happy to use higher powers in its treatment of the cubic, as does the work of Diophantus, published much earlier (although the notation here is odd). On the other hand Wikipedia mentions on the entry of La Geometrie that the ancient Greeks had a tradition of using length/areas/volumes for powers as shown. I suspect the reason why Descartes was so happy with this view of multipication is that it allowed him to express such algebraic problems geometrically, whereas previously no such interpretation could be found – and of course with the classical view of geometry as the foundations of mathematics, this was considered to be very important. tl;dr: For 2000 years humanity’s best mathematicians stymied by their inability to conceive of the concept of *multiplying four things together*, some guy you’ve never heard of named Descartes solves the problem in half a page.
A bunch of odd conversations about mathematics after Secular Solstice– mostly picking apart the strange and autodidactic opinions of @winged-light-blog, which I still don’t understand, (this happens when you do the right thing and don’t trust your maths teachers)– reminded me of the little I know about the Ancient Greeks’ approach to mathematics. Their worldview was interesting enough that I’d thought I’d share them with the world, at least so we can appreciate how much about maths we moderns take for granted and don’t realise involve nontrivial insights.
To Euclid and Archimedes and the rest of them, a number was a length, and, usually, any operations you were allowed to perform on numbers you had to be done with the old fashioned tools of a compass and straightedge, which led to problems when they tried to do things like trisect angles or square circles.
But where this way of thinking really got them stuck was how they thought about multiplication. You could multiply a length by a length, but you’d have to satisfy yourself with the answer being the area of a rectangle – an entirely different object. You’d prove that two areas are the same by some kind of dissection argument or something. You could multiply a length by an area, and get a volume. But if you tried to multiply a volume by something the response would be TYPE_ERROR, because geometry is about the real world and there are only 3 dimensions in the real world. And if to you tried to add a length to an area, or any funny business like that, the response would also be TYPE_ERROR, which is, I admit, a reasonable thing to do. (You could also, I think, multiply things by positive integers simply by adding them to themselves enough times, so that Euclid’s proof of the infinitude of primes still worked.) And for about 2000 years or so this is the way that western mathematicians thought, and this really screwed them over. They couldn’t talk about trying to solve equations with powers higher than the third – (anything fancy with exponentials or power series was, of course, right out). It was much easier to think of curves as loci of fancy constructions or conic sections than anything you could remotely compute anything with. And don’t forget that this was before modern mathematical notation, so you’d have to write all your operations out laboriously in Ancient Greek. It’s a wonder they got anything done at all.
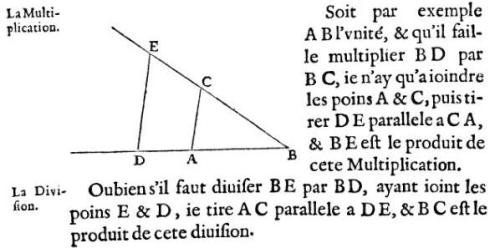
This whole complicated and annoying mess was finally resolved by Descartes. Yes, he of the fancy coordinate axes and “I think therefore I am”. On the way to basically inventing algebraic geometry and rendering almost all of ancient Greek geometry obsolete he deals with this problem in a few lines and a diagram.
First he declares by fiat that some random line segment is one (pretty much the same way that modern physicists declare that c, G, ħ and any other random constants they don’t like are 1 and that they can just rescale the units) Then he does some geometry with a pretty pair of similar triangles.
[Attempted translation: For example, letting AB be unity and wanting to multiply BD by BC, we need only join the points A & C and then draw DE parallel to AC. BE is then the product of the multiplication.]
And somehow you’ve multiplied a line by a line and gotten a line.
And from then on he just declares that he is allowed to do this as many times as he likes, and if he wants to take the 691st power of some line segment, so be it. And from there he was comfortable saying “This curve is the set of points satisfying x^23+ 59x^31y^3+y+47=0″ which would have made the ancient Greeks’ heads explode.
Descartes wasn’t terribly modest about his new invention of coordinate geometry, saying that “it compares to the Ancient Greek geometers like the rhetoric of Cicero compares to the ABCs of children”. And he probably should have considered the consequences of unleashing a new branch of maths onto the brains of unsuspecting university students.

(What algebraic geometry looks like today. This is scary and I don’t understand it and I don’t want to think about it) But however much of a douchebag he might have been about it, I do appreciate the ability to take 4th powers.
EDIT FOR BS: Looks like a hazy memory and some dubious sources make for an ridiculously overexaggerated story. @evolution-is-just-a-theorem Ars Magna (published a hundred years or so beforehand) seems happy to use higher powers in its treatment of the cubic and quartic. On the other hand Wikipedia mentions on the entry of La Geometrie that the ancient Greeks had a tradition of using length/areas/volumes for powers as shown. I suspect the reason why Descartes was so happy with this view of multipication is that it allowed him to express such algebraic problems geometrically, whereas previously no such interpretation could be found – and of course with the classical view of geometry as the foundations of mathematics, this was considered to be very important.
EDIT2: “There was an additional complication: the multiplication of lines was taken to produce surfaces, the multiplication of lines by surfaces to produce volumes, and the multiplication of surfaces to be meaningless; the square of a line was literally a square, and its cube literally a cube (Fig. 5.1). This limited the Greeks’ ability to deal with polynomials of more than the third degree.Weakening of Distinction. Partly under the influence of Arabic mathematics, the distinction be-tween numbers and magnitudes was beginning to weaken. For example,the brilliant Niccolò “Tartaglia” (The Stammerer) Fontana (c. 1500–1557)complained that some mathematicians were confusing multiplicare, the multiplication of numbers, with ducere, the multiplication of magnitudes. On the other hand, François Viète (1540–1603) argued that algebra was better then geometry, because it was not limited to equations of the third degree or lower. In fact, Descartes claimed that he began where Viète had stopped” So right that this was the Greeks’ view, right that Descartes rigorously resolved the issue at last, but there was a fair amount of groundwork needed to be laid before then – mathematicians had to get used to the idea of higher powers of reals, even though they didn’t quite have the justification for it. from https://web.eecs.utk.edu/~mclennan/Classes/UH267/handouts/WFI/c5.pdf cheers to @robustcornhusk
Never discuss infinity with a mathematician, they can go on about it forever.










Mathematical formulae may appear dry and inaccessible, but to a mathematician an equation can embody the quintescence of beauty. The beauty of a formula may result from simplicity, symmetry, elegance or the expression of an immutable truth. Professor Semir Zeki found that, as with the experience of visual or musical beauty, the activity in the brain is strongly related to how intense people declare their experience of beauty to be—even in this example where the source of beauty is extremely abstract. Read more.



Geometry & symmetry
Calculus was created to predict the rotation of the planets. I think you can bother to simplify your fractions.
Calculus professor (via mathprofessorquotes)
I really hate posts that have “there is no algebra in real life” and similar things that mention maths and it’s lack of application to reality. I also hate the fact that they are lauded as relatable, and get a lot of notes. If it wasn’t for algebra, calculus, and all forms of maths, and science, you would absolutely not be able to do 90% or more of what you do. Maths is the universal language and it really is beautiful. Without maths, you can’t have electricity, you can’t drive a car, use your computer, use the Internet, watch a movie, play a video game, use literally any program, have a house that doesn’t collapse, trains and public transport, plumbing, heating, furniture, air travel, statistics, so so so much more, and let’s not forget, that without maths, we would know nothing about space and would absolutely not be able to go there. If we extend this to science, this list would be exponentially longer. So please, don’t insult maths and it’s importance to our progress as humans, and its extensive application to every aspect of daily life. Many of us do use algebra in real life and strive to make your life better through its use.

-
 sealgairebeacan liked this · 7 months ago
sealgairebeacan liked this · 7 months ago -
 sockidemic liked this · 11 months ago
sockidemic liked this · 11 months ago -
 bananaede reblogged this · 1 year ago
bananaede reblogged this · 1 year ago -
 bananaede liked this · 1 year ago
bananaede liked this · 1 year ago -
 chairytale liked this · 1 year ago
chairytale liked this · 1 year ago -
 groovy-gyros reblogged this · 1 year ago
groovy-gyros reblogged this · 1 year ago -
 groovy-gyros liked this · 1 year ago
groovy-gyros liked this · 1 year ago -
 sandwitch-byte liked this · 2 years ago
sandwitch-byte liked this · 2 years ago -
 kaseyofthefields liked this · 3 years ago
kaseyofthefields liked this · 3 years ago -
 sadlittlecookie liked this · 3 years ago
sadlittlecookie liked this · 3 years ago -
 albertriemann reblogged this · 3 years ago
albertriemann reblogged this · 3 years ago -
 trietdo reblogged this · 4 years ago
trietdo reblogged this · 4 years ago -
 aberranthoughts reblogged this · 4 years ago
aberranthoughts reblogged this · 4 years ago -
 a-celestial-spark liked this · 4 years ago
a-celestial-spark liked this · 4 years ago -
 chimerical-charisma reblogged this · 4 years ago
chimerical-charisma reblogged this · 4 years ago -
 chimerical-charisma liked this · 4 years ago
chimerical-charisma liked this · 4 years ago -
 clocks-with-socks-united reblogged this · 4 years ago
clocks-with-socks-united reblogged this · 4 years ago -
 clocks-with-socks-united liked this · 4 years ago
clocks-with-socks-united liked this · 4 years ago -
 daijhane liked this · 4 years ago
daijhane liked this · 4 years ago -
 halfblindpirate liked this · 4 years ago
halfblindpirate liked this · 4 years ago -
 quin-is-a-fruit liked this · 4 years ago
quin-is-a-fruit liked this · 4 years ago -
 trvrbrkr liked this · 4 years ago
trvrbrkr liked this · 4 years ago -
 trossbass liked this · 4 years ago
trossbass liked this · 4 years ago -
 spookyskellington liked this · 4 years ago
spookyskellington liked this · 4 years ago -
 pallid-etoiles liked this · 4 years ago
pallid-etoiles liked this · 4 years ago -
 darth13 liked this · 5 years ago
darth13 liked this · 5 years ago -
 tenaciousbonkegggoth liked this · 5 years ago
tenaciousbonkegggoth liked this · 5 years ago -
 usn51 liked this · 5 years ago
usn51 liked this · 5 years ago -
 qlosher-blog liked this · 5 years ago
qlosher-blog liked this · 5 years ago -
 bbillster liked this · 5 years ago
bbillster liked this · 5 years ago -
 i-love-jack-o-lanterns liked this · 5 years ago
i-love-jack-o-lanterns liked this · 5 years ago -
 kizerron3 liked this · 5 years ago
kizerron3 liked this · 5 years ago -
 brendasoko-blog liked this · 5 years ago
brendasoko-blog liked this · 5 years ago -
 a-k-ron liked this · 6 years ago
a-k-ron liked this · 6 years ago -
 sknnyverse liked this · 6 years ago
sknnyverse liked this · 6 years ago -
 quincunx liked this · 6 years ago
quincunx liked this · 6 years ago
