Calculus Was Created To Predict The Rotation Of The Planets. I Think You Can Bother To Simplify Your

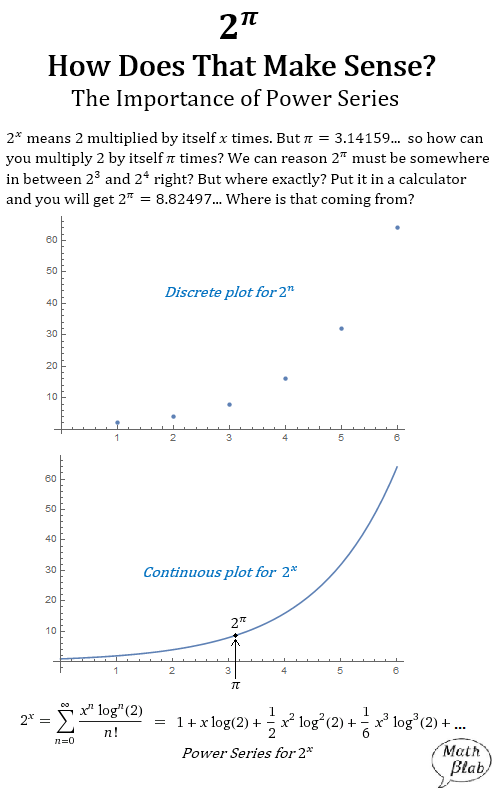
How can you multiply 2 by itself π times? Your calculator can do it. But how can we make sense of it? When x is a whole number 2^x makes sense and we can extend this thinking to get a feel for what the values of 2^x should be when x is in between two whole numbers. But how can we be more exact?

Visually, we can take a discrete graph of 2^x (a discrete graph is like a scatterplot) and try to draw a nice smooth curve through the points. This then traces out values of 2^x for any number x (including π). This idea has a rigorous mathematical framework called analytic continuation. What this means is that 2^x can be expressed equivalently as a power series and we can find those weird powers of 2 exactly by using the power series representation of 2^x. In fact, this is how most calculators find a decimal approximation for 2^π. The power series is an infinite sum, but adding up many terms in the power series gives a good approximation (above with π pluged in for x). The more terms added the better the approximation.

Mathematicians have also taken this idea to assign values to factorials other than 1!, 2!, 3!,… In other words, there is a way to compute π!

Mathematical formulae may appear dry and inaccessible, but to a mathematician an equation can embody the quintescence of beauty. The beauty of a formula may result from simplicity, symmetry, elegance or the expression of an immutable truth. Professor Semir Zeki found that, as with the experience of visual or musical beauty, the activity in the brain is strongly related to how intense people declare their experience of beauty to be—even in this example where the source of beauty is extremely abstract. Read more.

did humans invent math or did we discover it

does math even exist

What do you call a snake that’s exactly 3.14 feet long? 

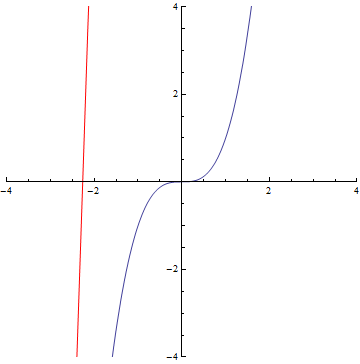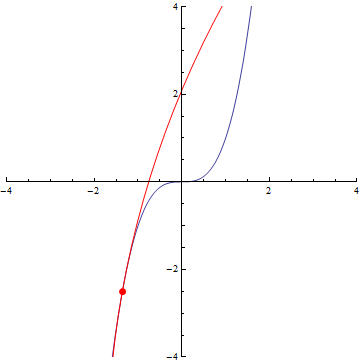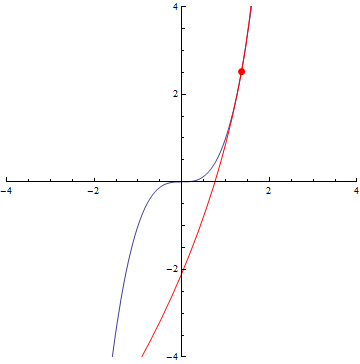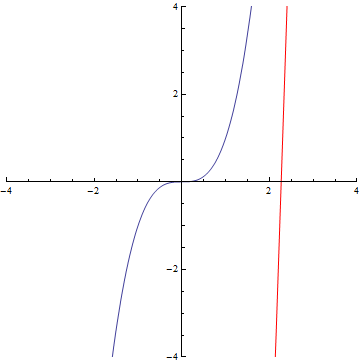
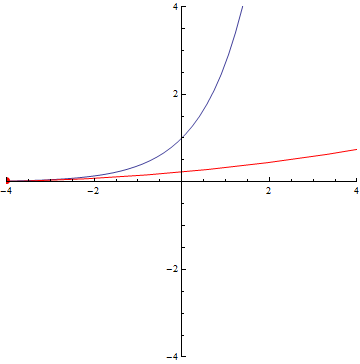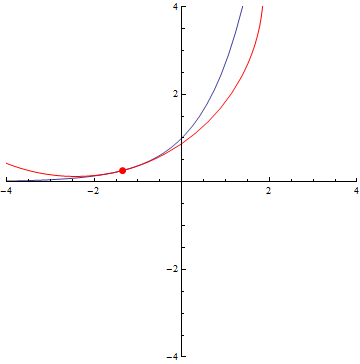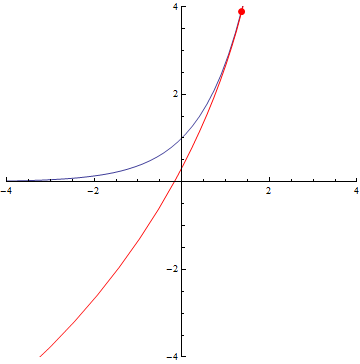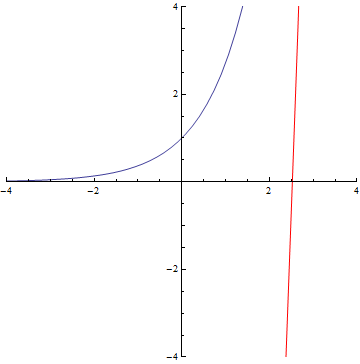
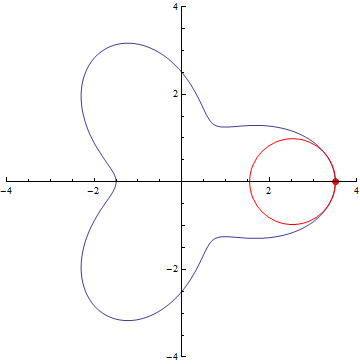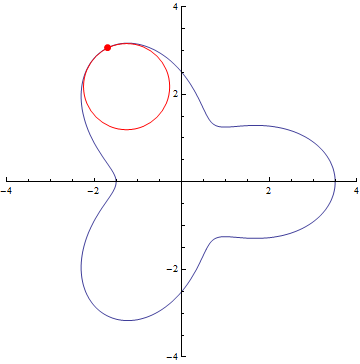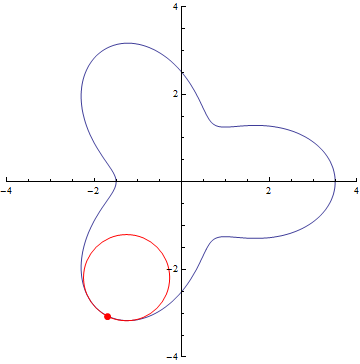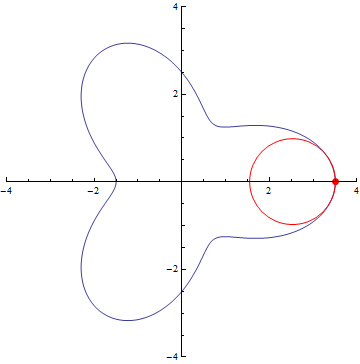
The curvature of curves.

x²

x³

sin(x)

exp(x)

Normal distribution (y=exp(-x²/2))

Ellipse

r=5/2+cos(3τθ)

x=(t-1)(t+1), y=t(t-1)(t+1)

Archimedes’ Spiral

Logarithmic spiral

If you want to try your own curve, try on Desmos graphing calculator!

https://www.desmos.com/calculator/lpm3igzbhy

New Largest Prime Revealed By Computer After Four-Month Delay

I find it hilarious that the computer which made this discovery actually kept it a secret for four whole months. Source: 

“The first thing to understand is that mathematics is an art. The difference between math and the other arts, such as music and painting, is that our culture does not recognize it as such.“

“There is surely no more reliable way to kill enthusiasm and interest in a subject than to make it a mandatory part of the school curriculum.”

“No mathematician in the world would bother making these senseless distinctions: 2 ½ is a “mixed number,” while 5/2 is an “improper fraction.” They’re equal for crying out loud.”

“All metaphor aside, geometry class is by far the most mentally and emotionally destructive component of the entire K-12 mathematics curriculum. Other math courses may hide the beautiful bird, or put it in a cage, but in geometry class it is openly and cruelly tortured. (Apparently I am incapable of putting all metaphor aside.)“

“A proof, that is, a mathematical argument, is a work of fiction, a poem. Its goal is to satisfy. A beautiful proof should explain, and it should explain clearly, deeply, and elegantly. A well-written, well-crafted argument should feel like a splash of cool water, and be a beacon of light— it should refresh the spirit and illuminate the mind. And it should be charming.“

“A proof should be an epiphany from the Gods, not a coded message from the Pentagon.“

“Students learn that mathematics is not something you do, but something that is done to you.“

This guy gets it

[EXTR4T3RR35TR14L W4LLP4P3R].

Mathematics is beautiful. <3

The coevolution of physics and math

Breakthroughs in physics sometimes require an assist from the field of mathematics—and vice versa.

tl;dr

[The] relationship between physics and mathematics goes back to the beginning of both subjects; as the fields have advanced, this relationship has gotten more and more tangled, a complicated tapestry. There is seemingly no end to the places where a well-placed set of tools for making calculations could help physicists, or where a probing question from physics could inspire mathematicians to create entirely new mathematical objects or theories.

I really hate posts that have “there is no algebra in real life” and similar things that mention maths and it’s lack of application to reality. I also hate the fact that they are lauded as relatable, and get a lot of notes. If it wasn’t for algebra, calculus, and all forms of maths, and science, you would absolutely not be able to do 90% or more of what you do. Maths is the universal language and it really is beautiful. Without maths, you can’t have electricity, you can’t drive a car, use your computer, use the Internet, watch a movie, play a video game, use literally any program, have a house that doesn’t collapse, trains and public transport, plumbing, heating, furniture, air travel, statistics, so so so much more, and let’s not forget, that without maths, we would know nothing about space and would absolutely not be able to go there. If we extend this to science, this list would be exponentially longer. So please, don’t insult maths and it’s importance to our progress as humans, and its extensive application to every aspect of daily life. Many of us do use algebra in real life and strive to make your life better through its use.