mexmath

Latest Posts by mexmath

“Poetry is a sort of inspired mathematics, which gives us equations, not for abstract figures, triangles, squares, and the like, but for the human emotions.”

— Ezra Pound (b. 30 October 1885)

A list of math books

…to read in lieu of an actual math class. So far I have

- Gödel, Escher, Bach: An Eternal Golden Braid by Douglas Hofstadter

- I am Strange Loop by Douglas Hofstadter

- Chaos by James Gleick

- Category Theory by Steve Awodey

“You ask me if an ordinary person by studying hard would get to be able to imagine these things like i imagine. Of Course!..I was an ordinary person who studied hard. There is no miracle people. It just happened they got interested in these things and they learned all these stuff. They’re just people!!There is no talent special miracle ability to understand quantum mechanics or a miracle ability to imagine electromagnetic fields that comes without practice and reading and learning and mathematics. So if you say you take an ordinary person whose willing to devote a great deal of time on studying and thinking and mathematics and so on. Then he’s become a scientist!” -Richard Feynman

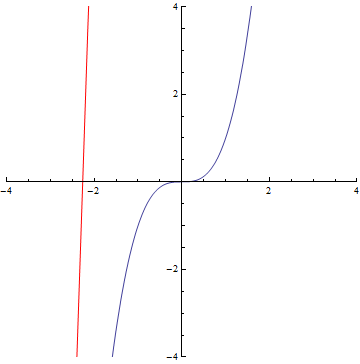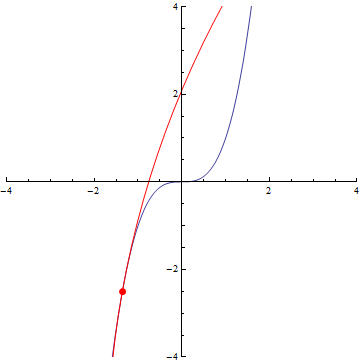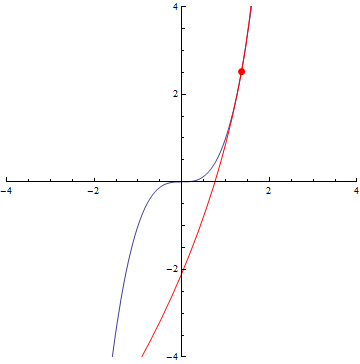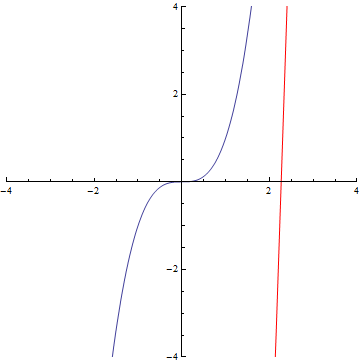
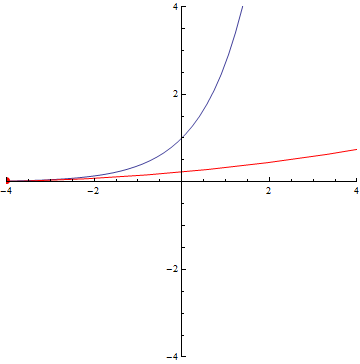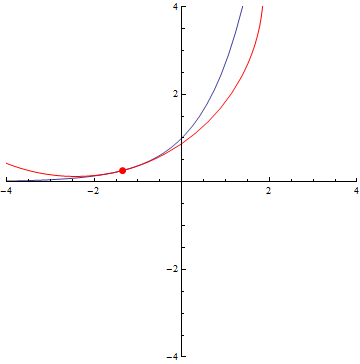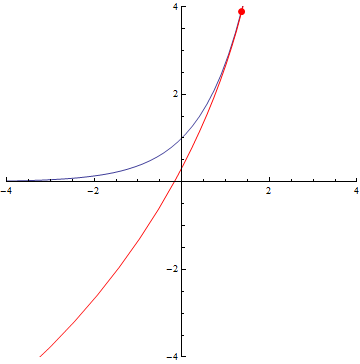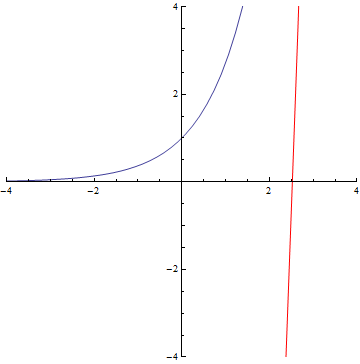
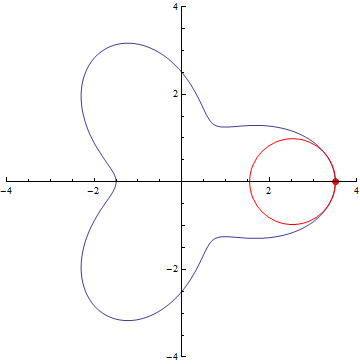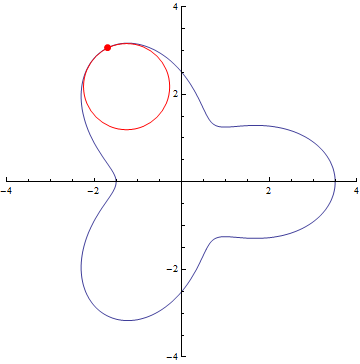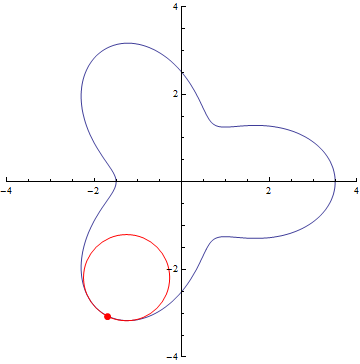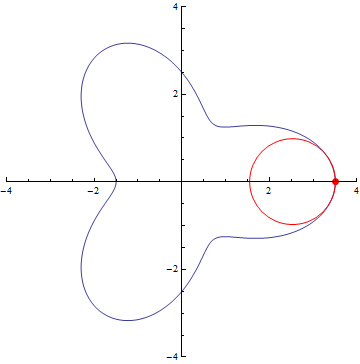
The curvature of curves.

x²

x³

sin(x)

exp(x)

Normal distribution (y=exp(-x²/2))

Ellipse

r=5/2+cos(3τθ)

x=(t-1)(t+1), y=t(t-1)(t+1)

Archimedes’ Spiral

Logarithmic spiral

If you want to try your own curve, try on Desmos graphing calculator!

https://www.desmos.com/calculator/lpm3igzbhy

Fun fact:

Green’s Theorem was discovered by two different mathematicians, independently, both in 1828. One (George Green) was English and the other (Mikhail Ostrogradsky) was Russian. We call it Green’s because

(a) it’s easier to remember, and

(b) no one in the past 500 years has named anything after a non-Englishman when there was an opportunity to name it after an Englishman.

Do you have any tips for exploring math ahead of my current classes that i am taking? I love everything about math and would like to gain some knowledge through non-school means

Hey! Thanks for the ask! 

A lot of this depends on whether you’d be interested in looking into things in a broad sense, which might have details which are too technical to understand at this stage, or if you’d prefer to actual learn further maths with full details and get better at it overall. When I was at school, I preferred to do the former, but the latter can also help make everything a lot more satisfying.

Note that everything below will be UK-centric, since that’s where I live!

Popular Maths Books

Personally, I loved to read “popular science” books a lot, since they often give overviews of a lot of topics but in a way that makes sense. A few of my favourites were:

-Norm Chronicles - David Spiegelhalter (I’ve actually got a signed copy of this one now, since he’s my Stats lecturer!)

-Sex by Numbers - David Spiegelhalter

-Alex’s Adventures in Numberland - Alex Bellos (plus the follow up Alex Through the Looking Glass)

-Things to Make and Do in the Fourth Dimension - Matt Parker

-Not a personal favourite, but anything by Ian Stewart is usually quite popular: I know I used to find his books a bit too full on for light reading however. He also writes a lot of university level books, which are very good, I just don’t think he’s so good at simplifying. Having said that, I did enjoy The Magical Maze

-Anything by Rob Eastaway is also top quality

But honestly, if you’re anywhere near a book shop, they usually have Popular Science books available, so have a browse to see what you think looks good to you!

In addition, here’s the pre-undergrad reading list for Cambridge: can’t say I’ve read everything on it, but it’s bound to have some decent things on it.

Youtube

I was never that big on Youtube, however there are a lot of channels out there which talk about maths. The ones I can think of off the top of my head are:

-Numberphile

-Matt Parker

-James Grime

Undoubtedly, there will be loads more than this: you can occasionally find talks given by people on there as well. One of my faves is Hannah Fry, but these are other things which you’ll probably come across by browsing a bit!

Podcasts

Two podcasts which I used to listen to a lot, and still do occasionally are:

-Infinite Monkey Cage (occasional maths episodes, but also a lot of good science)

-More or Less

Attending talks

I live within a reasonable range on London, so this is potentially more reasonable for me than others, but often universities and science societies host cheap or free talks. In the UK, the Royal Society are very good, as are the Royal Institute: but also keep an eye on any academic institutions near you, academics love talking about things they’re good at ;)

Attempting hard questions

If you ever feel like doing questions which are within your range of knowledge but also a bit more challenging/extensive than your curriculum, I can recommend:

-Nrich

-STEP Questions (aaaaa!)

Getting good at more “academicy” stuff

Honestly, for this there’s nothing I can recommend more for this than finding a textbook that looks like it’s a little bit of a stretch for you, and working all the way through it. If you get to a point where you run out of ideas of things to learn, there’s a brilliant set of lecture notes here, which start at early university level content (anything prior to that, I suspect teachers will have good suggestions for!)

I’m sure I’ll have missed something useful here, but I imagine people will also suggest things in the notes :D

Daily reminder that pi is really fucking cool

Once when lecturing in class Lord Kelvin used the word ‘mathematician’ and then interrupting himself asked his class: ’Do you know what a mathematician is?’

Stepping to his blackboard he wrote upon it the above equation.

Then putting his finger on what he had written, he turned to his class and said, ‘A mathematician is one to whom that is as obvious as that twice two makes four is to you.’

Top 10 Most Uncomfortable Math Facts

The only other thing that might surpass the weirdness of physics is the mind-bending, headache-inducing nature of math. So, here’s my top 10 unsettling math facts, along with brief explanations of what they mean.

10: i^2 = -1

Imaginary numbers feel like they shouldn’t exist to begin with. After all, what would it mean to have 4+5i apples? Although they don’t make much sense in the real world, complex numbers are incredibly useful, and pave the way for even stranger math.

9: d/dx e^x = e^x

The function y=e^x is a strange one, because if you plotted the slope as a function of x, you would get y=e^x. Also, if you plotted the area underneath the line as a function of x, you would get y=e^x again! Aside from y=0, this is the only function that is a plot of its own area and slope.

8: 1 + ½ + 1/3 + ¼ + 1/5 + … = ∞ 

Even though each term in the harmonic series gets smaller and smaller, the sum still goes off to infinity. Although this seems counter-intuitive, there’s a simple proof for it. It’s easy to see that the harmonic series is larger than 1 + ½ + ¼ + ¼ + 1/8 + 1/8 + 1/8 + 1/8 + …, which can be written as 1 + ½ + 2/4 + 4/8 + …, or 1 + ½ + ½ + ½ + …, which clearly goes to infinity. Since the harmonic series is larger, it too must tend to infinity.

7: Some infinities are bigger than others

You’d think that there’s nothing bigger than infinity, but this isn’t exactly the case. If you tried to pair off every natural number (1,2,3, …) with an irrational number (sqrt(2), e, π, …), you would find that there would always be some irrational numbers left over. This means that the infinite number of natural numbers is smaller than the infinite number of irrational numbers.

6: The halting problem

Imagine there’s a program H that can check to see if another program will run forever or not. Now let’s say there’s another program P. When P runs, it will use H to check if P will run forever or not. P then takes the result, and does the opposite of what it says. But this means that H didn’t correctly predict what P would do, which is a contradiction! So, H must be an impossible program to start with.

5: Russell’s paradox

Let’s say there’s a barber who only shaves everyone who doesn’t already shave themselves. Does the barber shave himself? If not, then he’s missing one person who doesn’t shave them self, but if so, he breaks his rule. This is the idea behind Russell’s paradox, which opened up a major contradiction in set theory that could only be fixed by changing axioms.

4: Fractal dimensions

Fractals are probably one of the most beautiful parts of math, but they can be very difficult to describe. A main issue is that fractals don’t have a clear number of dimensions. For instance, a Koch curve has zero volume if you tried measuring it using 2 dimensions, but it has an infinite length if you tried using 1 dimension. This isn’t very useful, so we instead use something in between 1 and 2 dimensions. It turns out, a Koch curve has about 1.26 dimensions.

3: e^(iπ) + 1 = 0

Euler’s identity is probably one of the most famous and beautiful math formulas that exist, combining e, i, and π all into a short equality. More generally, the formula is e^(ix) = cos(x) + i sin(x), derived from the series expansion e^x = 1 + x + x^2/2 + x^3/3! +… . Although this might be the most elegant, I wouldn’t say this is the most uncomfortable math fact that exists.

2: i^i is real

Going straight from Euler’s identity, we can quickly prove something even more strange. We know that e^(iπ/2) = cos(π/2) + i sin(π/2) = i, so we can raise each side to the power i to get i^i = e^(i*iπ/2), or e^(-π/2). From this, we can say that i^i ≈ 0.208. Somehow, raising an imaginary number to an imaginary number makes a real number!

1: Gödel’s incompleteness theorems

These two theorems are tied for first, both stating the limitations of math as a whole. The first incompleteness theorem states that there will always be true mathematical statements that can never be proven. This gives mathematicians nightmares, since some facts of math can never be known for certain, and we have no way of figuring out which ones they are.

The second theorem is even scarier, though, which states that arithmetic can never be proven to be consistent. This basically means that all of math could be wrong, but the only way to be certain would be to find some contradiction. If math does work, we’ll never know it.

“The first thing to understand is that mathematics is an art. The difference between math and the other arts, such as music and painting, is that our culture does not recognize it as such.“

“There is surely no more reliable way to kill enthusiasm and interest in a subject than to make it a mandatory part of the school curriculum.”

“No mathematician in the world would bother making these senseless distinctions: 2 ½ is a “mixed number,” while 5/2 is an “improper fraction.” They’re equal for crying out loud.”

“All metaphor aside, geometry class is by far the most mentally and emotionally destructive component of the entire K-12 mathematics curriculum. Other math courses may hide the beautiful bird, or put it in a cage, but in geometry class it is openly and cruelly tortured. (Apparently I am incapable of putting all metaphor aside.)“

“A proof, that is, a mathematical argument, is a work of fiction, a poem. Its goal is to satisfy. A beautiful proof should explain, and it should explain clearly, deeply, and elegantly. A well-written, well-crafted argument should feel like a splash of cool water, and be a beacon of light— it should refresh the spirit and illuminate the mind. And it should be charming.“

“A proof should be an epiphany from the Gods, not a coded message from the Pentagon.“

“Students learn that mathematics is not something you do, but something that is done to you.“

This guy gets it

The coevolution of physics and math

Breakthroughs in physics sometimes require an assist from the field of mathematics—and vice versa.

tl;dr

[The] relationship between physics and mathematics goes back to the beginning of both subjects; as the fields have advanced, this relationship has gotten more and more tangled, a complicated tapestry. There is seemingly no end to the places where a well-placed set of tools for making calculations could help physicists, or where a probing question from physics could inspire mathematicians to create entirely new mathematical objects or theories.

What can science tell us about history repeating itself?

Poincaré Recurrence theorem

The Poincaré recurrence theorem states that certain finite systems will, after a sufficiently long but finite time, return to a state very close to the initial state.

The  Poincaré recurrence time tells you how long one should wait for the recurrence to occur.

Now if we churn out the numbers for a hypothetical box containing a black hole with the estimated mass of the entire universe . the Poincaré recurrence time comes out too be this special number:

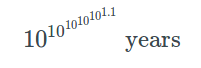
If we abstract ourselves from the possibility of experimentally testing it out, the key takeaway from this is that the Poincaré recurrence time is a finite number and one does not need to wait forever to observe the recurrence of events in the universe.

Therefore in Physics it does not make any physical sense to talk beyond this time scale.

Great question! Thanks for asking!

Source: Information Loss in Black Holes and/or Conscious Beings? by Don Page  - Please read this if you would like to know how that number was derived.

What is a Wormhole?

Wormholes were first theorized in 1916, though that wasn’t what they were called at the time. While reviewing another physicist’s solution to the equations in Albert Einstein’s theory of general relativity, Austrian physicist Ludwig Flamm realized another solution was possible. He described a “white hole,” a theoretical time reversal of a black hole. Entrances to both black and white holes could be connected by a space-time conduit.

In 1935, Einstein and physicist Nathan Rosen used the theory of general relativity to elaborate on the idea, proposing the existence of “bridges” through space-time. These bridges connect two different points in space-time, theoretically creating a shortcut that could reduce travel time and distance. The shortcuts came to be called Einstein-Rosen bridges, or wormholes.

Certain solutions of general relativity allow for the existence of wormholes where the mouth of each is a black hole. However, a naturally occurring black hole, formed by the collapse of a dying star, does not by itself create a wormhole.

Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist remains to be seen.

A wormhole could connect extremely long distances such as a billion light years or more, short distances such as a few meters, different universes, or different points in time

For a simplified notion of a wormhole, space can be visualized as a two-dimensional (2D) surface. In this case, a wormhole would appear as a hole in that surface, lead into a 3D tube (the inside surface of a cylinder), then re-emerge at another location on the 2D surface with a hole similar to the entrance. An actual wormhole would be analogous to this, but with the spatial dimensions raised by one. For example, instead of circular holes on a 2D plane, the entry and exit points could be visualized as spheres in 3D space.

Science fiction is filled with tales of traveling through wormholes. But the reality of such travel is more complicated, and not just because we’ve yet to spot one.

The first problem is size. Primordial wormholes are predicted to exist on microscopic levels, about 10–33 centimeters. However, as the universe expands, it is possible that some may have been stretched to larger sizes.

Another problem comes from stability. The predicted Einstein-Rosen wormholes would be useless for travel because they collapse quickly.

“You would need some very exotic type of matter in order to stabilize a wormhole,” said Hsu, “and it’s not clear whether such matter exists in the universe.”

But more recent research found that a wormhole containing “exotic” matter could stay open and unchanging for longer periods of time.

Exotic matter, which should not be confused with dark matter or antimatter, contains negative energy density and a large negative pressure. Such matter has only been seen in the behavior of certain vacuum states as part of quantum field theory.

If a wormhole contained sufficient exotic matter, whether naturally occurring or artificially added, it could theoretically be used as a method of sending information or travelers through space. Unfortunately, human journeys through the space tunnels may be challenging.

Wormholes may not only connect two separate regions within the universe, they could also connect two different universes. Similarly, some scientists have conjectured that if one mouth of a wormhole is moved in a specific manner, it could allow for time travel.

Although adding exotic matter to a wormhole might stabilize it to the point that human passengers could travel safely through it, there is still the possibility that the addition of “regular” matter would be sufficient to destabilize the portal.

Today’s technology is insufficient to enlarge or stabilize wormholes, even if they could be found. However, scientists continue to explore the concept as a method of space travel with the hope that technology will eventually be able to utilize them.

source

source

images: x, x, x, x, x, x, x, x, x

I mean, if it’s that easy to get a theorem named for you … “a straight line that passes through the center of a coplanar circle always divides the circle into two equal halves.” Can I have that one? Wait, can I auction off the naming rights? It can be the Red Bull Theorem or the Quicken Loans Theorem, depending who wants it more.

Rolle’s Theorem [Explained]

Ada Lovelace

Augusta Ada King, Countess of Lovelace (10 December 1815 – 27 November 1852) was an English mathematician and writer, chiefly known for her work on Charles Babbage’s proposed mechanical general-purpose computer, the Analytical Engine. She was the first to recognise that the machine had applications beyond pure calculation, and published the first algorithm intended to be carried out by such a machine. As a result, she is sometimes regarded as the first to recognise the full potential of a “computing machine” and the first computer programmer.

When she was a teenager, her mathematical talents led her to a long working relationship and friendship with fellow British mathematician Charles Babbage, also known as “the father of computers”, and in particular, Babbage’s work on the Analytical Engine. Lovelace first met him in June 1833, through their mutual friend, and her private tutor, Mary Somerville.

Book Recommendations: 

1) “The Thrilling Adventures of Lovelace and Babbage” by Sydney Padua

The book presents a delightful alternate reality in which Lovelace and Babbage do build the Difference Engine and use it to create runaway economic models, battle the scourge of spelling errors, explore the wider realms of mathematics and, of course, fight crime - for the sake of both London and science. Extremely funny and utterly unusual, it comes complete with historical curiosities, extensive footnotes and never-before-seen diagrams of Babbage’s mechanical, steam-powered computer.

2) “Ada Lovelace: Computer Wizard of Victorian England” by Lucy Lethbridge 

Daughter of the poet Lord Byron, Ada Lovelace was a child prodigy. Brilliant at maths, she read numbers like most people read words. In 1834 she came to the attention of scientist Charles Babbage, who had just built an amazing ‘thinking machine’. Thus began a remarkable collaboration in the invention of computer.

These books are also recommended for children. Target age: 10+

Celebrating Pascal’s birthday!

Blaise Pascal was a very influential French mathematician and philosopher who contributed to many areas of mathematics. He worked on conic sections and projective geometry and in correspondence with Fermat he laid the foundations for the theory of probability.

If you are interested in printing this as a poster for your class send me an email to lthmathematics@gmail.com so I can send you a pdf (easy for print).

The simulation hypothesis or simulation theory proposes that all of reality, including the Earth and the universe, is in fact an artificial simulation, most likely a computer simulation.

Weapons of Math Destruction | Book Review

Weapons of Math Destruction | Book Review

If you have been following me on social media, you probably know that I finished “Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy” by Cathy O’Neil. This was the book chosen in the LThMath Book Club (on Goodreads and Facebook) for the April and May 2019 reading challenge.

Overview

This book review is split into different parts for your convenience.

General…

View On WordPress

The Aesthetic Beauty of Math

The best mathematics, like the best literature, will continue to cause intense emotional satisfaction to thousands of people after thousands of years.

André Weil and G. H. Hardy views on mathematical beauty.

A mathematician, like a painter or a poet, is a maker of patterns,” he wrote. “If his patterns are more permanent than theirs, it is because they are made with ideas.” Hardy went on to characterize what makes a mathematical idea worthy: a certain generality, a certain depth, unexpectedness combined with inevitability and economy.

See Hardy’s essay A Mathematician’s Apology (wiki, PDF, Amazon)

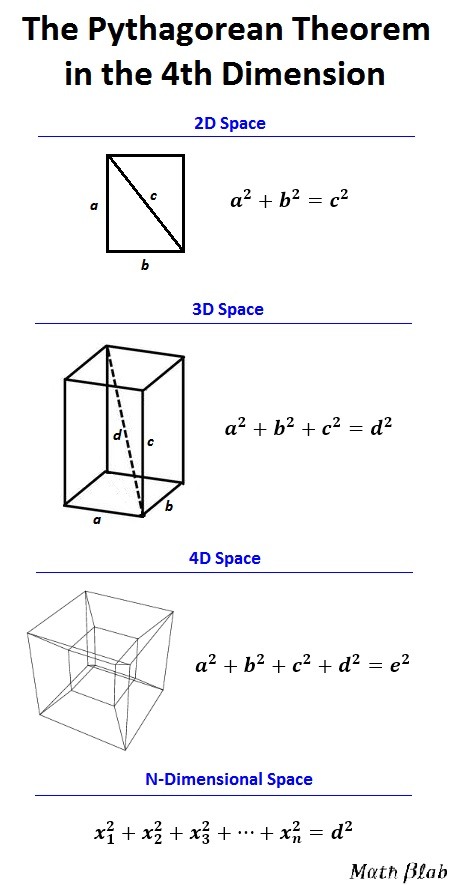
The Pythagorean theorem can be extended to any number of dimensions. In 2D space, the Pythagorean theorem gives us the length of the diagonal of a rectangle. It turns out, a simple modification (adding another square term) to the formula gives the diagonal of a rectangular prism. In the same way, the formula can be further extended to apply to 4 dimensional situations, and give the diagonal of a hypercube (4D cube) or tesseract (yes that’s where Marvel got the name for that glowing blue cube, one of the infinity stones). Keeping with the pattern, the Pythagorean theorem can be generalized to any arbitrary whole number dimension to apply to finding diagonals of n-dimensional rectangle analogs. 
 Okay, but is this 4th dimension, hypercube stuff even real? IDK, is any math real? It doesn’t matter. But I can tell you this type of mathematics is useful. For example, these formulas are used to calculate lengths of vectors and are used in statistics to calculate standard deviation. Also Einstein’s theory of general relativity relies on a 4-dimensional mathematical framework. Without knowing this, the GPS in your phone would not work (GPS relies on precise timing, so precise that the effects of earths mass on spacetime become necessary to consider). 
 See also Weisstein, Eric W. “Tesseract.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/Tesseract.html

[EXTR4T3RR35TR14L W4LLP4P3R].

Mathematics is beautiful. <3

I mean, you could do this with logic… like a primitive human.

Electrical engineering prof on the merits of VHDL

[Mathematics is] a very powerful and effective language invented by humans to describe and discover patterns in nature. When we perceive beauty in the mathematics, I think what we’re really perceiving is an underlying beauty in nature itself.

Jim Baggott, Quantum Space

153 - A Narcissistic Number

153 is a narcissistic number–a number that can be generated from its own digits (so it’s obsessed with itself? hence the narcissism?) like so:

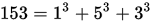
More precisely, a narcissistic number is a natural number that is the sum of its own digits each raised to the power of the number of digits. So since 153 has 3 digits, each digit is cubed and then summed together. There are only four 3-digit  narcissistic numbers:

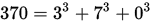
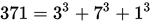
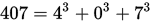
A very interesting thing about narcissistic numbers is that, unlike may other sets of numbers (e.g., even/odd numbers, prime numbers, triangular numbers, etc.), there are only finitely many of them. In base 10, there are only 88 (10 of them being the 1 digit numbers). The largest narcissistic number has 39 digits, this guy:

115,132,219,018,763,992,565,095,597,973,971,522,401 

Why is this? Essentially, the sum cannot keep up with the size of the number. More info here: https://en.wikipedia.org/wiki/Narcissistic_number

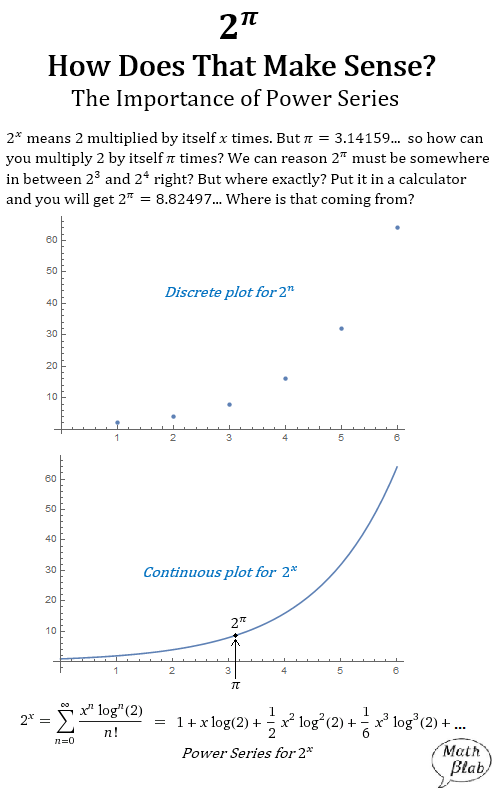
How can you multiply 2 by itself π times? Your calculator can do it. But how can we make sense of it? When x is a whole number 2^x makes sense and we can extend this thinking to get a feel for what the values of 2^x should be when x is in between two whole numbers. But how can we be more exact?

Visually, we can take a discrete graph of 2^x (a discrete graph is like a scatterplot) and try to draw a nice smooth curve through the points. This then traces out values of 2^x for any number x (including π). This idea has a rigorous mathematical framework called analytic continuation. What this means is that 2^x can be expressed equivalently as a power series and we can find those weird powers of 2 exactly by using the power series representation of 2^x. In fact, this is how most calculators find a decimal approximation for 2^π. The power series is an infinite sum, but adding up many terms in the power series gives a good approximation (above with π pluged in for x). The more terms added the better the approximation.

Mathematicians have also taken this idea to assign values to factorials other than 1!, 2!, 3!,… In other words, there is a way to compute π!