Your Window to Inspiration: Seamlessly Browse Tumblr!
Mathematics - Blog Posts
Lissajous curves 😍
I remember learning about them fo the first time and thinking they were useless pretty curves, oh how wrong I was!
Now, to me they highlight the importance of resonances on dynamical systems and join number theory with differential equations while being hella cute
I love them


Be chaotic, and never know anything

RESONANCES! They affect everything!

Every 11 years, the Sun cycles through from riotous flare and sunspot activity to a quieter period, before ramping up again. It’s almost as regular as clockwork, and for years astronomers have been wondering what causes it. Now, they’ve proposed a new solution.
Even though the Solar System’s planets are much smaller than the Sun, the gravity of some of them is able to influence our star’s magnetic field. This, the researchers assert, is what controls the solar cycle.
Venus, Earth, and Jupiter assert a small gravitational tug on the Sun as they orbit it. The result is comparable to the way the Moon’s gravity influences Earth’s tides, producing a regularly timed ebb and flow.
The team has traced back 1,000 years of solar cycles, between the years 1000 and 2009 CE, comparing that data against the movements of the planets in that time. They found an impressively strong link between the two.
“There is an astonishingly high level of concordance: what we see is complete parallelism with the planets over the course of 90 cycles,” said physicist Frank Stefani of the Helmholtz-Zentrum Dresden-Rossendorf in Germany.
“Everything points to a clocked process.”
What the team found is that the tidal forces are strongest when Earth, Venus, and Jupiter align, and that this alignment occurs every 11.07 years - falling at the same time as the solar minimum.
Continue Reading.


The topologist’s sine curve.
Limts: f(x)=sin(1/x) is a rare example of a function with a non-existent one-sided limit. More technically, f(x)=sin(1/x) is defined for all numbers greater than zero, yet the limit as x approaches zero from the right of f(x)=sin(1/x) does not exist. This can be reasoned by considering the value of f at x-values near zero. Informally, f(near zero) could be 1 f(just a bit closer to zero) could be -1 so f(numbers near zero) does not seem to settle on a single y-value.
Continuity: Note that f is continuous for all numbers greater than zero but not continuous at x=0 since f is undefined there. Even if we were to “fill in the bad point” and let f(0)=0, the function would still not be continuous at zero! (note this is the natural choice as sin(0)=0). We can see that the adjusted f is still not continuous at zero since the sequence x_n=1/(pi/2+npi) converges but f(1/x_n) is the sequence (-1)^n which does not converge. This is similar to the argument above. In other words, closing in on x=0, we can keep finding x values such that f(x)=-1 and f(x)=1.
Topology: In topology, the topologist’s sine curve is a classic example of a space that is connected but not path connected. This space is formed in R^2 by taking the graph of f(x)=sin(1/x) together with its limit points (the line segment on the y-axis [-1,1], the red line on the second image). The graph of f is connected to this line segment as f and the segment cannot be sepearted by an open disc (no matter how small). This can be informally reasoned by the zooming illustration in the second image. But the space is not path connected by the sequence argument above (there is no path to the point (0,0)).
Image credits: http://mathworld.wolfram.com/TopologistsSineCurve.html and https://simomaths.wordpress.com/2013/03/10/topology-locally-connected-and-locally-path-connected-spaces/

https://twitter.com/dreugeniacheng/status/1097969617014804480?s=21

Unexpected great discoveries. Calculating the cosmos: How mathematics unveils the universe. By Ian Stewart.
Chaos: When the present determines the future, but the approximate present does not approximately determine the future
Edward Lorenz
GEOMETRY THEY COULD NEVER MAKE ME LOVE YOU. NEVER.
not to be a number nerd on main but 2025 (45^2) will be the only square year most of us ever experience. the last one was 1936 and the next one will be 2116
galois is so funny. solve a 350 year old math problem at 19. lay the foundations of group theory, also at 19. get taken as political prisoner. go to prison for several months. immediately enter a duel upon being freed and die
my handwriting before coffee:

my handwriting after coffee:

Yeah I'm in the maths fandom but I don't really engage with the source material as much as I used to, y'know? I'll go back and read the classics but even then not recently and honestly I vibe so much harder with the place the fanfics are going.
My favorite example of girl math is when David Hilbert and Albert Einstein couldn't solve how energy conservation worked in general relativity, so Hilbert asked Emmy Noether about it and she solved it for them.
Are Complex Numbers Really Numbers?
If you look through definitions of “number” most will say that numbers are used to represent quantities (amounts or measures). Whole numbers 0, 1, 2, 3, … are probably the first numbers that come to mind and they are often used to count things like say how may watermelons jimmy has. But when quantifying things like money, whole numbers are not always enough and so we have rational numbers (which include the whole numbers but also fractions and numbers with finite or repeating decimal expansions). Yet, sometimes even these numbers are not enough to express certain quantities. Pi, for example, is not a rational number but is certainly a number as it represents the quantity that is the ratio of a circle’s circumference to its diameter. It can be shown that the number pi has an infinite decimal expansion with no repeating patterns, and so a number like pi is called an irrational number. (Because they are silly? Although at first some thought so, the term irrational just means not rational.) More specifically, pi is a transcendental number as it is not the root of any polynomial. (Transcendental, because they transcend the usual notion of number? Idk. Again, strange names.) So, the rational numbers were extended to the real numbers to include both rational and irrational numbers. Either way, we see that both rational and irrational numbers are truly numbers since they can be used to represent quantities.
What about complex numbers though? Are they really numbers, or do people just call them “numbers”? So, we should ask, can complex numbers represent some amount or measure of something? Can jimmy have i watermelons? No, but jimmy can’t really have pi watermelons either and pi is a number. Jimmy may have a watermelon that weighs pi pounds though (the only way to know this would be if jimmy had a scale with infinite accuracy, which, turns out, he does). Okay but can jimmy have a watermelon weighing i pounds? That doesn’t seem to make sense. To see if complex numbers can represent quantities we need to elaborate on what complex numbers are exactly.
The complex numbers are the real numbers extended to include the square root of negative 1 (i) and all its multiples. They have the form a+bi where a and b are real numbers. i is called an imaginary number (named imaginary because, i is not a real number, but this implies numbers like i are somehow not “real”, in the usual English sense of the word (are any numbers really “real”?) again, with the names). What truly makes complex numbers different than the other numbers we have discussed is that they “live” in 2 dimensions (the complex plane); complex numbers (e.g., 7+2i) have a real part (7) and an imaginary part (2i). While real numbers (which include whole, rational, and irrational numbers) “live” in one dimension (they can be found anywhere on the number line).
So, a complex number is a sort of two-dimensional quantity, it has a real measure and an imaginary measure. This makes them strange as numbers. We know 12 is bigger than 11 and that there are a bunch of numbers in-between 11 and 12, but which is bigger 2-8i or 3+i? Complex numbers cannot be compared in the same way i.e., there is no way to order complex numbers from smallest to largest.
These properties make complex numbers more abstract than typical numbers we encounter day to day. Nevertheless, “complex numbers are useful abstract quantities that can be used in calculations and result in physically meaningful solutions. However, recognition of this fact is one that took a long time for mathematicians to accept.”—Wolfram MathWorld http://mathworld.wolfram.com/ComplexNumber.html
The math trick that college will never teach you! : Parametric Integration
Parametric integration is one such technique that once you are made aware of it, you will never for the love of god forget it. It goes by many names : ‘Differentiation under the Integral sign’, ‘Feynman’s famous trick’ , ‘Parametric Integration’ and so on.
Let me demonstrate :
Now this integral might seem familiar to you if you have taken a calculus course before and to evaluate it is rather simple as well.

Knowing this you can do lots of crazy stuff. Lets differentiate this expression wrt to the parameter in the integral – s (Hence the name parametric integration ). i.e


Look at that, by simple differentiation we have obtained the expression for another integral. How cool is that! It gets even better.
Lets differentiate it once more:


.
.
.
If you keep on differentiating the expression n times, one gets this :

Now substituting the value of s to be 1, we obtain the following integral expression for the factorial. This is known as the gamma function.

There are lots of ways to derive the above expression for the gamma function, but parametric integration is in my opinion the most subtle way to arrive at it. :D
This is a really powerful technique and I strong suggest that if you have taken calculus, then please do read this article.
Have a great day!
EDIT: It had to be gamma(n+1) not gamma(n) .Thank you @mattchelldavis

Can you flatten a sphere?
The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.
This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.
The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.
If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.
However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.
The Dymaxion map projection.
The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.
One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.
The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.
So what does this flattened sphere approximated by conical strips look like? Check the image below.
But this is not the only way to distribute the strips. We could also align them by a corner, like this:
All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.
It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!
Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

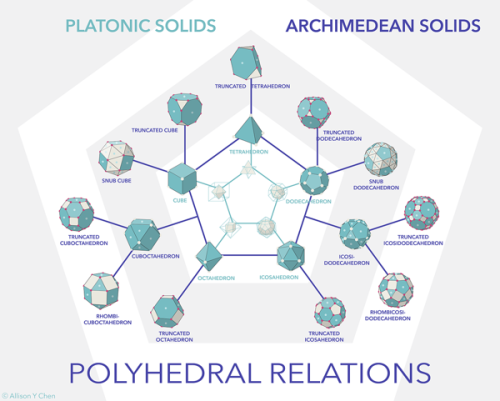
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.
An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.
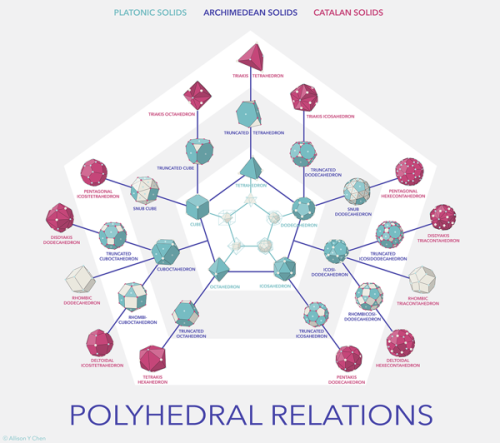
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.
The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.
Images: Polyhedral Relations by Allison Chen on Behance.
3/14 Pi Day, School Walkout, Stephen Hawking, and more
A lot happening today! I just wanted to post a couple of updates and thoughts...
Before I had breakfast this morning I heard the word that Stephen Hawking had passed away. What an amazing human being, such an incredible loss for the world. And what an amazing coincidence for him to die on Einstein’s birthday...

Stephen Hawking
Stephen Hawking Taught Us a Lot About How to Live (NYT)
Stephen Hawking Dies at 76; His Mind Roamed the Cosmos (NYT Obituary)
Stephen Hawking: Visionary physicist dies aged 76 (BBC)
This is the most dangerous time for our planet (Stephen Hawking 12/16)
Stephen Hawking Was Right To Worry About Our Impending Doom (io9)
Stephen Hawking’s most mind-blowing discovery: black holes can shrink: Hawking radiation, explained by a physicist. (Vox)
Stephen Hawking’s 5 best and nerdiest pop culture cameos: When Hawking wasn’t changing the world, he played himself on TV. He was hilarious. (Vox)
Pi Day
I always look forward to Pi Day... friends usually send me Pi Day pictures and animated gifs... I wore my new Pi shirt to PT today and I’ve finally updated my Pi Page :) You can also check out my new Flickr post on Pi Day...

School Walkout
These two photos from the 17 photos from today's National School Walkout for gun control that should terrify the NRA are my favorite:


#NationalWalkoutDay on Twitter
Previous post on tumblr about gun violence

mood: filling an open set with dyadic cubes and pretending this is studying measure theory



Some group theory notes that I took today.
📚Summer Studying Challenge 📚
August 8 2021: What books are you currently reading?
Yesterday I started reading 1984 by George Orwell.But I have also started two other books namely 'Men of Mathematics' by E.T.Bell and 'Music Of Primes' by Marcus du Sautoy.I have also decided to buy Anna karenina by Tolstoy after reading a post about it by @theclassicalmind.

Today was a good day ^_^
I completed
The first chapter of Analysis 2.The first chapter is all about limits.
I also did half of chapter 13 of analysis 1.
I also solved like 15 problems of analysis 1.
I loved the chapter of power series.It was kinda cool.I also liked the chapter of limits.I am looking forward to study tomorrow's chapter ^_^
(PS:The picture is some old notes of group theory)


Heya! I finished chapter 12 of Analysis 1.It was I think the toughest chapter so far but it's not that tough that I'll loose my sleep over it.I also got the above book from Amazon today.The title is sexist but so is history 🤷🏻♀️I started from the last chapter and made some notes on it.I also revised chapter 8 today.Otherthan that it was a pretty chill day.I also answered an ask on Tumblr.I thought it was important to answer the question correctly and so I tried to the best of my ability 🐰
Now Nighty Nighty you guys
I hope you had a good day <3
Hello! I really like your blog and it somehow makes me feel good and safe, your notes are really pretty! When I look at them they seem so interesting and I wish to understand them but the problem is I haven't even started university (I have just finished high school) and I'm kind of scared thinking it would be too difficult for me to grasp. It is just so different from high school math but at the same much more fascinating. Do you perhaps have any advice on how to introduce myself to it, where to start? Or should I just wait for the classes to start and then study?Best wishes to you!! Thank you
Hey @dantesdream !
I just want you to know that mathematics is difficult at the University level but it is not more difficult than any other university course.It is just different.📚
So how is mathematics different and why you shouldn't get discouraged by it?
There is an entire book written on it.It is called 'Alex's Adventures in Numberland' written by Alex Bellos.There is one particular page that I really like.It talks about how are brain perceives the world around us on a logarithmic scale but mathematics is linear and that is why we have to put the extra effort into it (To convert logarithmic to linear) but according to me this extra effort is far less than wading through hundreds of textbooks often contradicting each other that many other university courses require. Here is the cover page of the book I recommended if you would like to read it.

Apart from having a positive attitude towards it I think it'll be great if you could start studying it before your university begins.
So from where should you start?
If you know where you'll be going for your university studies then you can check if your university has uploaded their notes online and start accordingly.Some old students also usually post their notes,so see if you can get your hands on them.If these two options fail then there are two more.Oxford university has made all their mathematics notes avalilable.You can start with their Introduction to mathematics and complex numbers course (I'll put the link at the end).A student from Cambridge University named Dexter Chua also has made his notes available.You can start with Numbers and sets if you use his notes (Again I'll put the link at the end).
Oxford notes:
https://courses.maths.ox.ac.uk/overview/undergraduate
Dexter's notes:
https://dec41.user.srcf.net/notes/
You should be fine with these but the beginning steps into mathematics needs a little more help.You can use the book called as 'How to prove it:A structured approach' by Daniel J. Velleman.If you can read this with the first course that you are taking (your university notes or Oxbridge notes) then I think you'll enjoy the course more just like I did.Here is the image of the book

If you want to know more then I'm just a message away so feel free to ask your doubts.
And thank you for all your compliments hehe ^_^

Heya!!
So today I just revised the first four easy chapters of analysis 1 and then I started chapter 12 (Analysis 1).Chapter 12 is about tests for convergent series like the leibinz test for alternating series,comparison tests (there are two of them) and a lot more which I will be doing tomorrow.I am feeling very tired today.I didn’t even do much.I just had 2 hours of statistics exam and have been feeling tired ever since.Maybe I did not rest enough after the exam or maybe I just have to go and sleep now.
I did place an order for some multivitamin pills though.This is the first time I’ll be using the brand so let’s just see how that goes and apart from that I telephoned two of my school teachers.Here in India it’s guru Poornima (Basically Teacher’s Day according to the Hindu calendar) and it was lovely talking to them.I really do miss them a lot.I also put a sheet mask on in the evening hoping that it’ll make me feel better.It did but I’m still tired so I’m just gonna go sleep.
Aww look at you cutie reading everything hehe I hope your day went better^_^
See you tomorrow <3

Heya!!
Today I revised all the topics I covered in Analysis 1 so far and did chapter 8 and 9.
Chapter 8 is about the algebra of limits.In there I learnt how to write proofs using ε-N method.There were quite a number of cases (with examples!).Most of them were good and could be deduced easily from previous theorems and axioms but I did find 4 proofs a little challenging.I have noted them down and I’ll be discussing those with my prof soon.
Chapter 9 was about monotonic sequences.In there I learnt about the monotonic sequence theorem and the proof of this theorem is very cute.This theorem's proof is very intresting because it connects to the theorem where square root of 2 is proved as irrational but it is more general.So it patches all the gaps on the real number line quit nicely.There were some examples too which I liked and I also learnt the steps of proving a theorem when monotonicity is involved.
It was a pretty cool day.
I hope you had a good day too^_^
***
The Mayuriit Project
Will I make it? Stay tuned to find out!
206 days left…




